Grade 2
General Outcome:
Develop number sense
Specific Outcome:
9. Demonstrate an understanding of addition (limited to 1-
and 2-digit numerals) with answers to 100 and the corresponding subtraction by:
- using personal strategies for adding and subtracting with and without the support of manipulatives
- creating and solving problems that involve addition and subtraction
- using the commutative property of addition (the order in which numbers are added does not affect the sum)
- using the associative property of addition (grouping a set of numbers in different ways does not affect the sum)
- explaining that the order in which numbers are subtracted may affect the difference.
- [C, CN, ME, PS, R, V]
My Solution:
Lance:
3 x 2 = 6 flowers
1 x 5 = 5 flowers
6 + 5 = 11 flowers
Lance has 11 flowers.
Betsy:
3 + 1 = 4 triangular pots
4 x 2 = 8 flowers
2 x 3 = 6 flowers
8 + 6 = 14 flowers
Betsy has 14 flowers.
Cara:
2 + 1 = 3 square pots
3 x 3 = 9 flowers
1 x 5 = 5 flowers
9 + 5 = 14 flowers
Cara has 14 flowers.
Possible student solutions:
Lance:
Betsy:
Cara:
Possible
errors:
When
solving for Lance’s number of flowers students could easily confuse the
different sets of data. When solving for
Lance in the following two examples, students correctly applied one set of data
but missed the other:
(Student
knew that the triangle had two flowers and that the circle had five, but forgot
that there were multiple pots)When solving for Betsy, students may not recognize the need to include data from the previous question:
Justification:
I chose this problem because I like how it requires students
to apply mathematical concepts to a more complex problem. The problem is easily differentiated: students
begin by solving for Lance, and can then move on to the more complex questions
regarding Betsy and Cara. Although at
first glance this problem may seem more appropriate for a higher grade (it is a
multiplication problem, after all), students are able to solve it using the
skills that they possess (multiplication is compiled addition).
Grade 4
General Outcome:
Use patterns to describe the world and solve problems.
Specific Outcome:
4. Identify and explain mathematical relationships, using charts and diagrams, to solve problems.
Question:
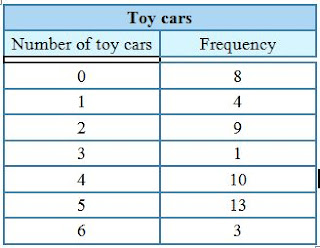
All of the students in the after school program were asked to bring toy cars to play with on a Thursday afternoon. Some kids forgot to bring cars, but many kids brought more than one car.
My Solution:
1) I looked at the chart and understood that it groups students by how many cars they brought. Because the question asked for how many people brought four cars, I found five on the chart and saw that the corresponding number is 10.
2) Again, because I understood the frequency chart, I found the number three in the right hand column and saw that six people all brought three cars.
3) I extended the chart by multiplying the number of cars by the number of people who brought that amount and took the sum of the answers:
0 x 8 = 0
1 x 4 = 4
2 x 9 = 18
3 x 1 = 3
4 x 10 = 40
5 x 13 = 65
6 x 3 = 18
0+4+18+3+40+65+18=148
The total amount of toy cars brought was 148.
Possible Student Solutions and Errors:
1) Confusion may arrise as to what the meaning of each column is. Therefore, one possible, but incorrect student answer would be 1. This would happen by finding the number 4 in the frequency column instead of number of cars column.
2) Again, due to a misunderstanding of how the information is shown in the chart, a student may have answered 1.
3) Some possible incorrect answers may include adding the frequency column, adding the number of cars column, or adding both columns. Students must have a good understanding of what frequency means in order to head towards the correct answer.
Justification:
I chose this problem because it can easily be differentiated; most students should be able to attempt the first two questions. The third question requires an understanding of the first two questions in order to find an answer. I also chose this problem to better familiarize myself with frequency charts and understand how they can be used, and how they can be taught.
Grade 6
General Outcome:
Use experimental or theoretical probabilities to represent and solve problems involving uncertainty.
Specific Outcome:
4. Demonstrate an understanding of probability by:
• identifying all possible outcomes of a probability experiment
• differentiating between experimental and theoretical probability
• determining the theoretical probability of outcomes in a probability experiment
• determining the experimental probability of outcomes in a probability experiment
• comparing experimental results with the theoretical probability for an experiment.
[C, ME, PS, T]
[ICT: C6–2.1, C6–2.4]
Question:
If you flip a coin 6 times, what is the best prediction possible for the number of times it will land on tails?
My Solution:
If you flip a coin one time, the probability that you will get tails is %50. If you flip a coin another time, the probability that you will get tails is still %50. That means after six flips, the probability that you will get tails is still %50. This means that %50 of the time the flips should be tails.
Possible Student Solutions and Errors:
Students would likely gravitate towards flipping a coin to test how many times it lands on tails. After several sets of six flips, students would likely come close to the fact that they will flip heads %50 of the time (experimental probability). Without, however, having an understanding of theoretical probability, there is still a possibility for a margin of error.
Justification:
I am personally interested in statistics and probability. I realize that my personal interests can both positively and negatively influence my class. However, because I get excited about coin flipping, I know that my students will too. I realized while thinking about this problem that it is important to be comfortable with terminology, possible questions, and have resources for answers. This probability website helped answer some of my questions.
Grade 4
General Outcome:
Use patterns to describe the world and solve problems.
Specific Outcome:
4. Identify and explain mathematical relationships, using charts and diagrams, to solve problems.
[CN, PS, R, V]
[ICT: C6–2.3]
Question:
All of the students in the after school program were asked to bring toy cars to play with on a Thursday afternoon. Some kids forgot to bring cars, but many kids brought more than one car.
1) How many people brought four toy cars?
2) Three people shared the same amount of toy cars. How many did they have?
3) How many toy cars were there in all?
My Solution:
1) I looked at the chart and understood that it groups students by how many cars they brought. Because the question asked for how many people brought four cars, I found five on the chart and saw that the corresponding number is 10.
2) Again, because I understood the frequency chart, I found the number three in the right hand column and saw that six people all brought three cars.
3) I extended the chart by multiplying the number of cars by the number of people who brought that amount and took the sum of the answers:
0 x 8 = 0
1 x 4 = 4
2 x 9 = 18
3 x 1 = 3
4 x 10 = 40
5 x 13 = 65
6 x 3 = 18
0+4+18+3+40+65+18=148
The total amount of toy cars brought was 148.
Possible Student Solutions and Errors:
1) Confusion may arrise as to what the meaning of each column is. Therefore, one possible, but incorrect student answer would be 1. This would happen by finding the number 4 in the frequency column instead of number of cars column.
2) Again, due to a misunderstanding of how the information is shown in the chart, a student may have answered 1.
3) Some possible incorrect answers may include adding the frequency column, adding the number of cars column, or adding both columns. Students must have a good understanding of what frequency means in order to head towards the correct answer.
Justification:
I chose this problem because it can easily be differentiated; most students should be able to attempt the first two questions. The third question requires an understanding of the first two questions in order to find an answer. I also chose this problem to better familiarize myself with frequency charts and understand how they can be used, and how they can be taught.
Grade 6
General Outcome:
Use experimental or theoretical probabilities to represent and solve problems involving uncertainty.
Specific Outcome:
4. Demonstrate an understanding of probability by:
• identifying all possible outcomes of a probability experiment
• differentiating between experimental and theoretical probability
• determining the theoretical probability of outcomes in a probability experiment
• determining the experimental probability of outcomes in a probability experiment
• comparing experimental results with the theoretical probability for an experiment.
[C, ME, PS, T]
[ICT: C6–2.1, C6–2.4]
Question:
If you flip a coin 6 times, what is the best prediction possible for the number of times it will land on tails?
My Solution:
If you flip a coin one time, the probability that you will get tails is %50. If you flip a coin another time, the probability that you will get tails is still %50. That means after six flips, the probability that you will get tails is still %50. This means that %50 of the time the flips should be tails.
Possible Student Solutions and Errors:
Students would likely gravitate towards flipping a coin to test how many times it lands on tails. After several sets of six flips, students would likely come close to the fact that they will flip heads %50 of the time (experimental probability). Without, however, having an understanding of theoretical probability, there is still a possibility for a margin of error.
Justification:
I am personally interested in statistics and probability. I realize that my personal interests can both positively and negatively influence my class. However, because I get excited about coin flipping, I know that my students will too. I realized while thinking about this problem that it is important to be comfortable with terminology, possible questions, and have resources for answers. This probability website helped answer some of my questions.










No comments:
Post a Comment